bolsover
Senior Member
Calculation of the involute is quite simple:
C#:
public static List<Point> InvolutePoints(double baseRadius, double tipRadius, int steps)
{
var points = new List<Point>(steps);
var stepSize = (tipRadius - baseRadius) / steps;
for (var i = 0; i < steps + 1; i++)
{
var step = baseRadius + i * stepSize; // dimension of current step
var alpha = Math.Acos(baseRadius / step);
var invAlpha = Math.Tan(alpha) - alpha; // involute function
var x = step * Math.Cos(invAlpha); // X coordinate
var y = step * Math.Sin(invAlpha); // Y coordinate
points.Add(new Point(x, y));
}
return points;
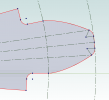
}The list of X,Y points is used to add a spline to the sketch.
There are a few complexities however..
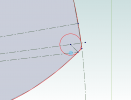
The root fillet is a simple arc. For some gears, the root fillet arc joins the involute above the base radius. To ensure the end of the root fillet arc and the start of the involute are at the same X,Y location requires interpolation. Taking each point on the involute, I check if this is within a circle from the gear centre to the top of the fillet arc. I keep doing this until a point is found outside the circle. I then create an interpolated point between the last involute point inside and the first outside the circle. This interpolated point is then the first point on the involute.
Here is the code that does the interpolation:
C#:
private int Intersect(Point CirclePos, double CircleRad,
Point LineStart, Point LineEnd, ref Point Intersection)
{
if (IsIntersecting(CirclePos, CircleRad, LineStart, LineEnd))
{
//Calculate terms of the linear and quadratic equations
var m = (LineEnd.Y - LineStart.Y) / (LineEnd.X - LineStart.X);
var d = LineStart.Y - m * LineStart.X;
var a = 1 + m * m;
var b = 2 * (m * d - m * CirclePos.Y - CirclePos.X);
var c = CirclePos.X * CirclePos.X + d * d + CirclePos.Y * CirclePos.Y -
CircleRad * CircleRad - 2 * d * CirclePos.Y;
// solve quadratic equation
var sqRtTerm = Math.Sqrt(b * b - 4 * a * c);
var x = (-b + sqRtTerm) / (2 * a);
// make sure we have the correct root for our line segment
if (x < Math.Min(LineStart.X, LineEnd.X) ||
x > Math.Max(LineStart.X, LineEnd.X))
{
x = (-b - sqRtTerm) / (2 * a);
}
//solve for the y-component
var y = m * x + d;
// Intersection Calculated
Intersection = new Point(x, y);
return 0;
}
// Line segment does not intersect at one point. It is either
// fully outside, fully inside, intersects at two points, is
// tangential to, or one or more points is exactly on the
// circle radius.
Intersection = new Point(0, 0);
return -1;
}David
