Hey Oldbelt,
To be honest I don't have it clear in my head how to translate the +1. I understand that a gearset with a 10t sun gear and a 40t ring gear is a 4:1 ratio when the ring gear is being driven, but needs 5 sun gear rotations in order to rotate the carrier once. Does that mean I actually need a 5:1 ratio to get the equivalent full carrier rotation or do I just end up with that? Even though it is a 4:1 gear set the actual input rotations to output rotations is 5:1. Thinking as I type, it seems what I actually need is a 6:1 gearset (with a 7:1 input/output) driving a 2:1 gearset (with a 3:1 input/output).
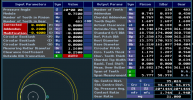
Input
driving carrier/input
driving carrier/output (as in the model in #7) resulting in a 21:1 reduction.
I freely admit that I may be wrong with this but.......
I didn't agree with your sentence
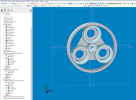
A planetary gear with 3 planet wheels must have a sun gear wheel where the amount of teeth's is a multiple of 3 as the first stage of the gearbox in #7 has 3 planetary gears and a sun gear with 23t, planetary gears with 37t and a ring gear with 97t. The modelled gearbox exists, we overhaul them regularly. Also the planetary gear is not even or the ring gear divisible by 3.
As I said, we really need to know the maximum diameter that the ring gear tooth root can be in order to determine what ratio is possible.
This is a 6:1 ratio with 23t sun gear. 1+138/23 = 7 which has a ring gear root od of 105.975
I've chosen 0.75M as the sun gear works out close to the 18mm given earlier.
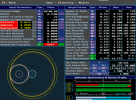
It's interesting that the modelled gearbox ratio in #7 is 97/23 = 4.217, giving a (+1) 5.217 ratio. Obviously power, torque and tooth strength as well as limiting dimensions all play a part in the final design of a planetary gearset.
I don't have to
be right, but I do want the
answer to be right.