有限要素解析入門

シミュレーションの重要な出力の一つは応力です。 応力は、単純に物体にかかる力を断面積で割ったものとして計算されます。 例えば、長方形の梁にかかるせん断応力の式は次のようになります：

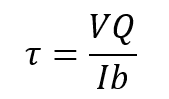
τ = 横荷重を受けた梁のせん断応力

V = せん断力

Q = 中立軸に関する面積の第一モーメント

I = 慣性モーメント

b = せん断力の方向における梁の幅

この計算は単純な長方形の場合だけだ。 このような形状の応力とひずみはどのように計算できるのでしょうか？

確かに単純な方程式では無理です。 FEA、特にコンピュテーショナル・アプローチが設計者に大きな利益をもたらすのはこの点です。

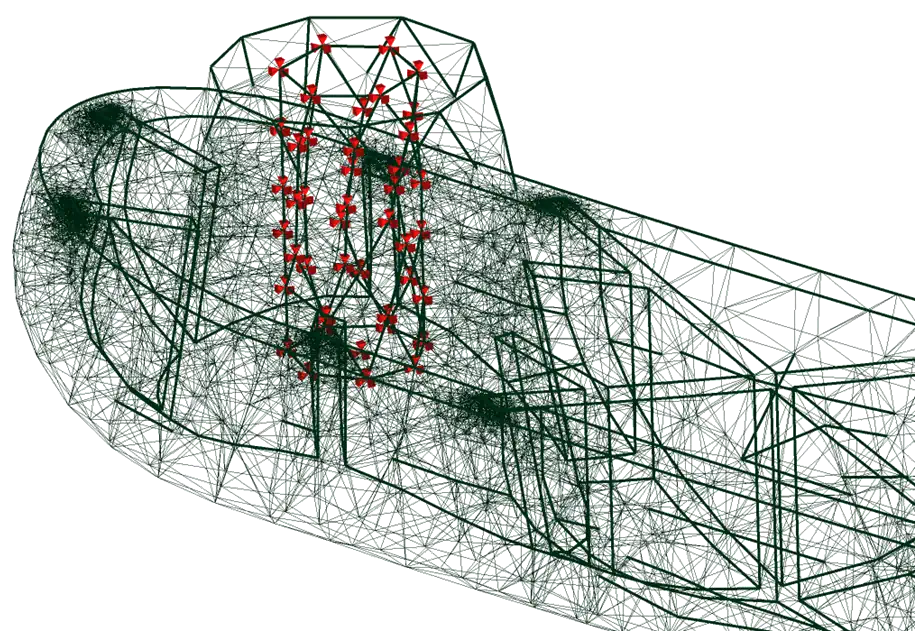
曲線的で有機的な複雑な形状を計算するのは難しいが、三角形による応力計算ははるかに簡単でわかりやすい。下の図は、手作業では計算が難しい曲線状の物体です。 このオブジェクトを近似的な三角形に分割し、角が接する部分に赤い点を付けます。 これらの点は「ノード」と呼ばれ、それぞれの赤い点で応力を計算することができます。これにより、問題を小さな、つまり有限の塊、「有限要素」に分解することができます。いくつかの種類のメッシュを生成することができます。

四面体メッシュは三角形要素（左）を使用し、六面体メッシュは四角形要素を使用する。 多くの場合、六面体メッシュが高精度で最も望ましい。 三角形は強度が高く、剛性が高い傾向にあるため、四面体メッシュで作成されたものは、実際よりも剛性が高く見えることがある。 しかし、四面体メッシュは、六面体よりも複雑で有機的な形状に効果的にフィットします。

メッシュは指数関数的な性質を持っており、メッシュ要素を増やせば増やすほど、つまり三角形が小さくなればなるほど、結果を得るために必要な計算量は指数関数的に増えていきます。 メッシュサイズと計算には相関関係があるため、最適なメッシュサイズについては多くの議論があります。 ほとんどの場合、研究の質や解像度を犠牲にすることなく、かつ解答に過大な時間がかからないようなメッシュサイズを選ぶようにしてください。

境界条件は、解析を定義するための基本的な入力です。 節点や面に適用できる条件であり、解析にどのような力を使うか、何を安定させるか、さらにはどのような温度にするかを指示します。 この例では、椅子の土台を解析してみましょう：

動かない形状を FEA に伝える必要があります。 この解析では、椅子の車輪と相互作用する面を固定します。 境界条件を使用することで、これらの面や節点は動かない、固定形状であることを解析ソフトウェアに伝えることができます。 境界条件の中には、ある方向には制限を反映するが、他の方向には制限を反映しないものもあります。

完全な解析を行うためには、椅子に座る人のシミュレーションも重要である。 座っている人の力を表す境界条件をもう一つ追加することができます。 椅子からの荷重を受ける面を選択し、下方向に力を加えることができます：

色彩は美しいが、分析はまだか？

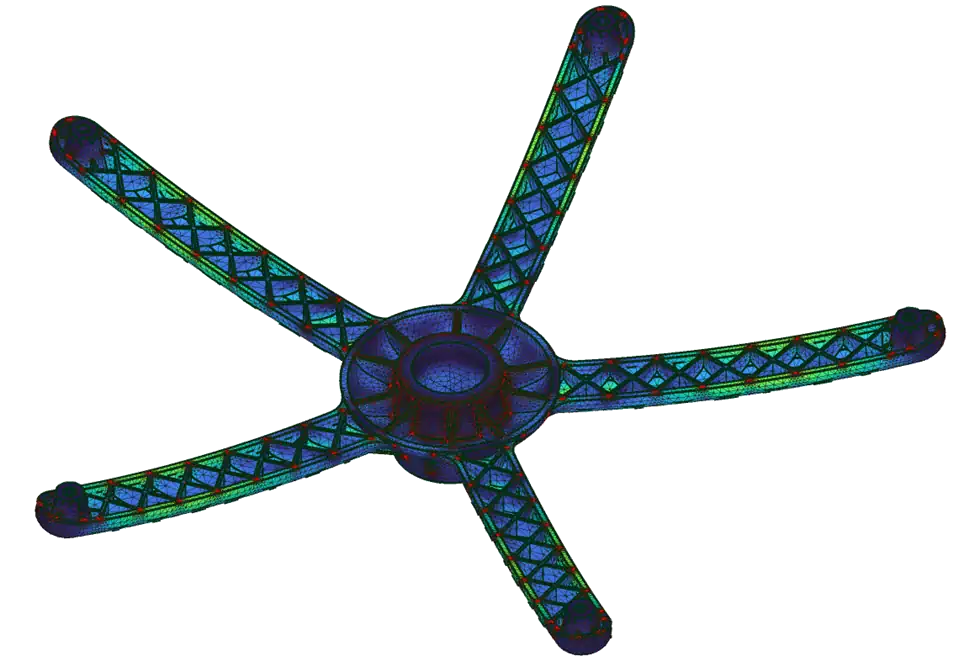
複雑な問題は、複雑な解決策を提示する可能性がある。 シミュレーションが実行されると、ほとんどのプログラムでは応力と変形の領域を示すカラースケールが強調表示されます。 また、部品の変形を誇張したアニメーションが表示されることもあります。これは、解析が期待通りの結果を出しているか、正しく設定されているかを視覚的に確認するためのものです。 多くのFEAシミュレーションでは反力も出力されます。結果を見るための重要な最初のステップは、反力の正味の値を取り、それが入力力を完全に打ち消すかどうかを確認することです。 そうでない場合は、シミュレーションのどこかにエラーがある可能性があります。

カラースケールは、応力や変形が最も大きい部分を示すためのものですが、通常は失敗か合格かを示すものではありません。 どんなに良い結果が出たとしても、FEAは方程式の一部に過ぎません。 本格的なFEAアナリストは、FEAの結果を裏付けるために、手作業で数学的モデリングを行うべきです。

エンジニアリングにおいて、FEAは設計と試験において重要な役割を果たしています。物理的なプロトタイプを作る前に、エンジニアが材料や部品の構造的な完全性や耐久性を評価することができます。

FEAは、建築物や橋梁、さらには機械部品の設計における構造解析に広く利用されています。FEAによる応力試験は、構造物の弱点や応力集中の特定に役立ちます。

応力や熱などの条件下で、さまざまな材料がどのような挙動を示すかを理解することは不可欠です。FEAはこれらの特性を解析するのに役立ち、より安全で効率的な設計を実現します。

FEAが構造解析に重点を置くのに対し、数値流体力学（CFD）は流体解析に用いられる。どちらも、航空宇宙や自動車工学のような分野、あるいは工学の産業応用が関係するあらゆる場面で極めて重要です。

有限要素解析は、単純な弾性問題を解くだけでなく、様々な複雑な解析を含みます：

弾性限界を超えた材料の挙動を解析する必要があるかもしれません。 これは非線形解析として知られています。 これは以下のような理由で発生します。

非線形材料の挙動：材料が解析を通してフックの法則に従わない。その代わりに、塑性、超弾性、クリープなど、応力とひずみの関係が線形でない挙動を示します。

幾何学的非線形：大きな変形や回転が発生し、負荷時に構造の形状が大きく変化します。これによりシステムの剛性マトリックスが変化し、荷重に対する構造の応答方法に影響を与える。

境界条件の非線形性：コンポーネント間の接触など、解析中の境界条件の変化。

これは、地震解析のように、時間的に変化する荷重に対して構造物がどのように応答するかを研究することである。 これは構造設計に大いに役立つ。

有限要素解析は、航空宇宙から土木工学まで、幅広い産業で応用されています。これらの応用例とFEAの今後の動向を探ってみよう。

自動車業界では、衝突安全性や燃費効率を解析することで、より安全で効率的な自動車を設計するためにFEAが使用されています。航空宇宙分野では、より軽量で強度の高い航空機部品の設計に役立っています。

有限要素解析（FEA）は、現代のエンジニアリングや設計に欠かせないツールとなっています。実環境をシミュレートし、さまざまな荷重下での構造物の挙動を予測できるFEAは、さまざまな産業で重宝されています。

物理的プロトタイピングの最小化：
製品設計の強化：
安全性と信頼性の向上：実際の配備前に潜在的な故障箇所を特定するのに役立ちます。

新興テクノロジーとの統合：3D
持続可能なエンジニアリング：FEA は、より持続可能で環境に優しい材料や設計の開発において重要な役割を果たしている。

計算能力の進歩：計算能力が向上するにつれて、より複雑で正確なシミュレーションが可能になります。

これまで述べてきたように、FEAは単なるエンジニアのためのツールではありません。 FEAは、設計における革新、安全性、効率性への入り口なのです。自動車設計であれ、航空宇宙工学であれ、材料科学であれ、FEAの役割は極めて重要であり、常に拡大しています。この強力なツールを理解し活用することで、エンジニアリングや設計のほぼすべての分野において、画期的な進歩と効率化を実現することができます。