Sketching Environment

Sketching profiles for features is a huge part of the design process. The sketching environment has to be great for you to be productive. You'll love ours.

Download Alibre Design

What is a profile sketch?

Sketches are 2D profiles that are used as the basis for most core 3D modeling operations. They contain sketch figures, dimensions, and constraints.

The workflow is typically to create one or more sketches and then to use a 3D modeling operation on them to create a solid. Most parts you make will have several or many profile sketches.

As a result, most of the time spent defining the core geometry and dimensions of your models will take place inside the various sketches of your 3D models.

In the example to the left, a sketch was created to define the profile of this component, and then an Extrude command turns the sketch profile into a 3D model.

Comprehensive Text Tools

Great text support is imperative for many designs. Enjoy support for nearly all well-designed fonts - be creative and adhere to brand requirements.

Instantly transform text along a path, such as a circle or spline for full creative control without any tedious letter positioning.

Color Coded Problem Areas

See the status of your sketch in real-time with color-coded feedback that tells you where you need to add more definition.

When all the sketch figures are black, you can be confident the model is fully defined, meaning no surprises later because of an oversight.

Point Import and Fitting

Sometimes your design must incorporate data from specialized external applications or maybe just an Excel file you've made yourself. Import points from a CSV and optionally fit the points with lines or a spline to successfuly use the geometry definition for your part.

Sketch Constraints

Constraints are geometric relationships between sketch figures that allow you to build design intent into your model. They are crucial to minimizing both effort and human error. Some include:

Symmetric

Coradial

Collinear

Vertical

Horizontal

Coincident

Intersect

Midline

Concentric

Tangent

Perpendicular

Parallel

Sketch Dimensions

Dimensions dictate the size and location of model components and can be created and freely modified at any point.

The freedom to rapidly modify dimensions of the model allows you to make significant changes to the model in a safe, predictable way as many times as you need to.

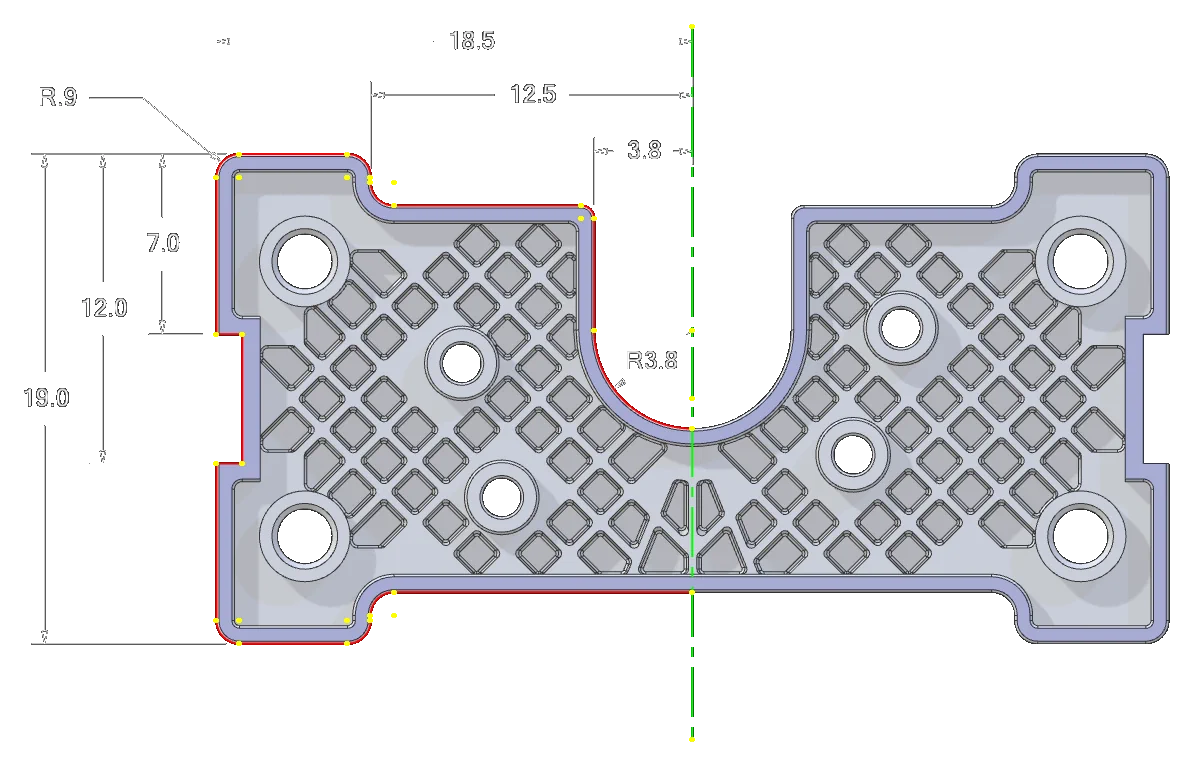
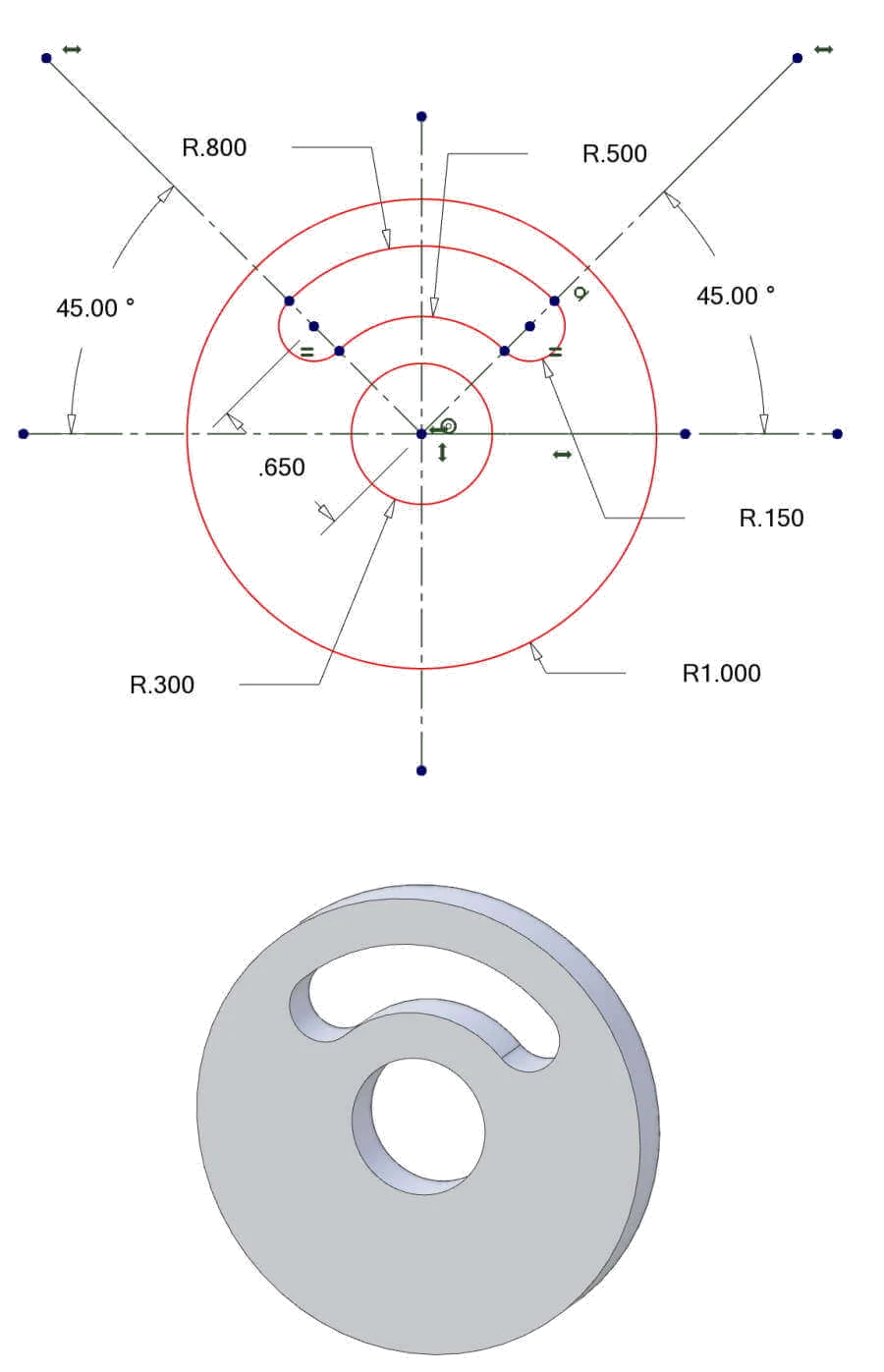
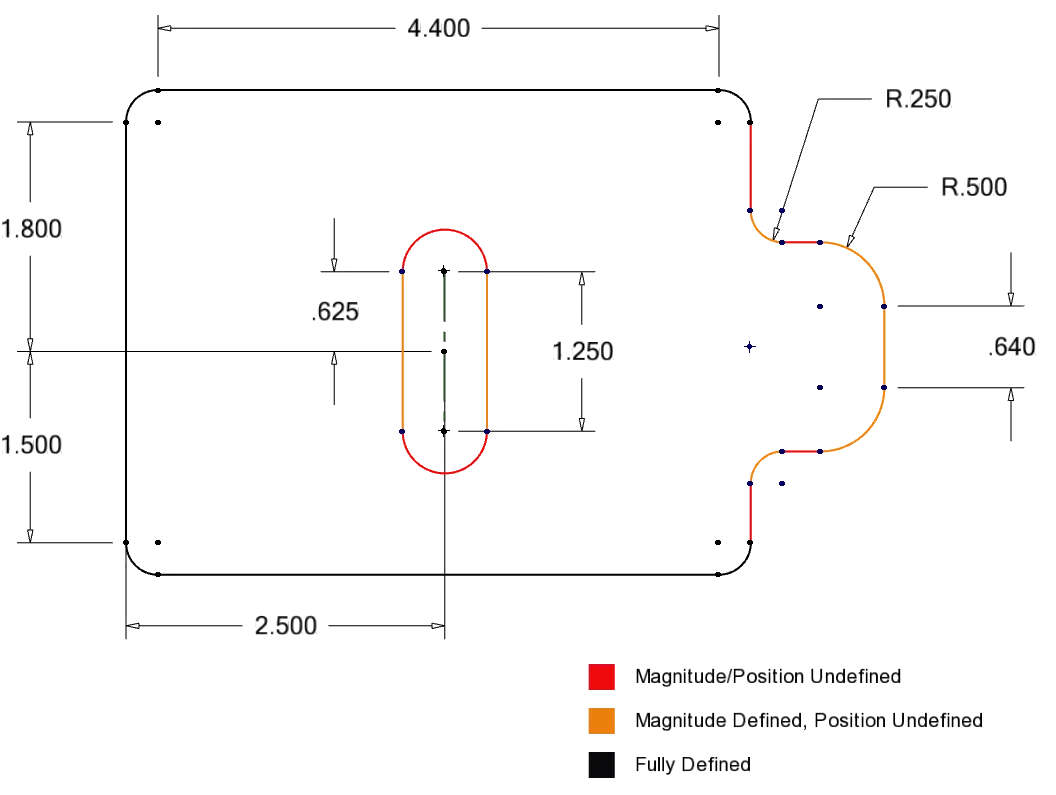
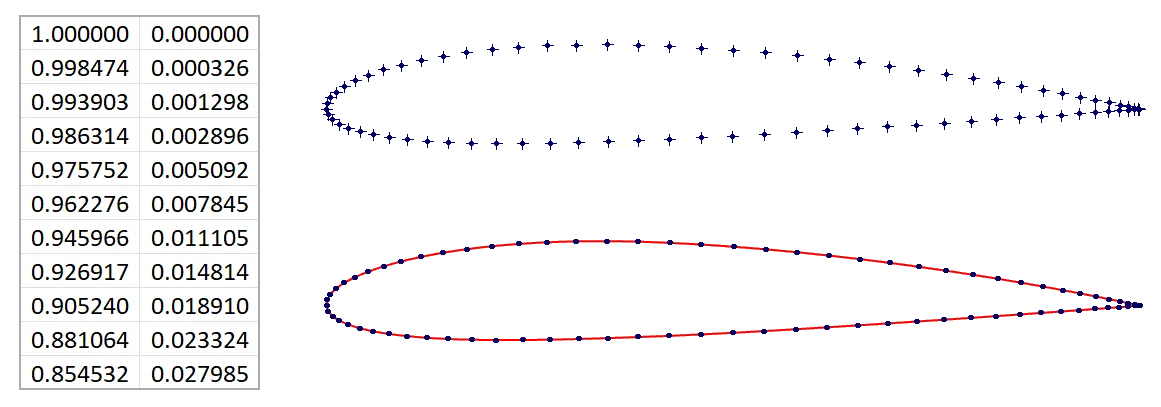
Using Equations in Sketches

Equations are just dynamic dimensions. You can create relationships and use those relationships to populate dimensions instead of using a fixed number.

For example, you can set a rectangle's Width = (2 x Height) - 2 and any changes to Height will update the Width value automatically.

Reusing Geometry (Projecting)

Creating every piece of sketch geometry from scratch is tedious and introduces unnecessary human error. Leverage existing model geometry and previously created sketches to form the basis of new sketches, significantly shortening sketch creation time and improving reliability.

Image Tracing

Use images as a visual reference while sketching. Set images to a known real-world size using the Calibration tool. Sketch on top of them to trace objects so they can be reproduced.

Use Tracing Images for reverse engineering or creative work.

Smart Popup Menus

Reducing mouse travel and seeing the right tools at the right time is key to efficiency. Smart menus speed up the most common sketch tasks by showing tools relevant to the selection right at the mouse.